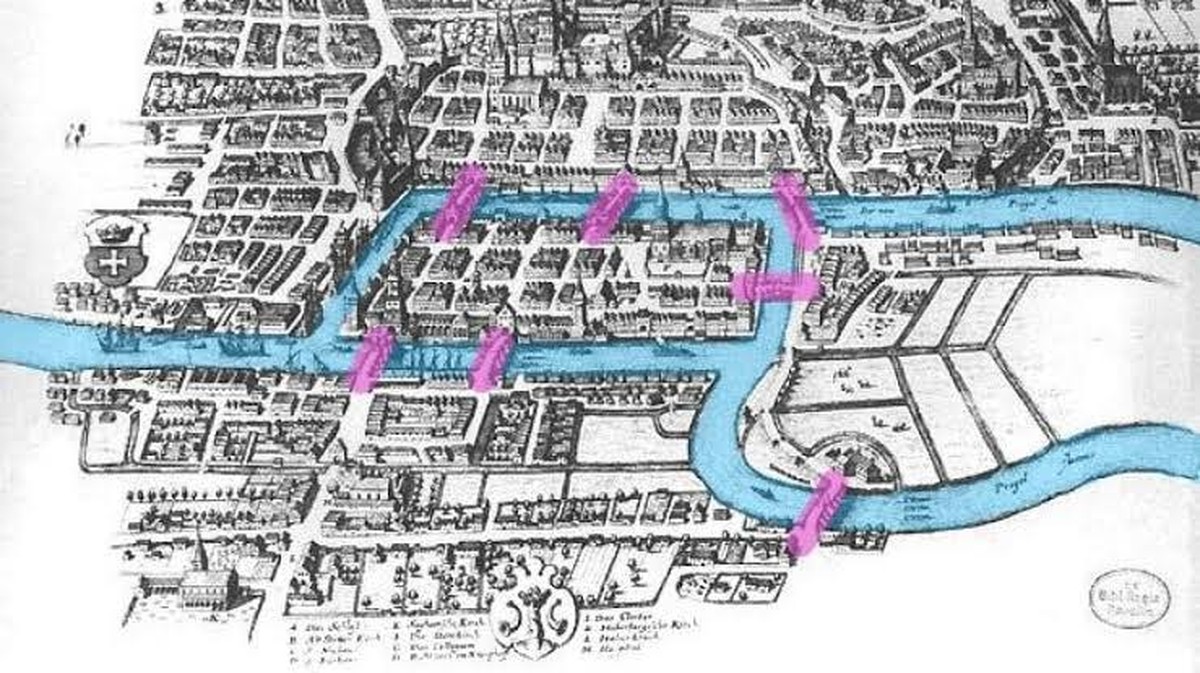
De voormalige Pruisische stad Königsberg, nu bekend als Kaliningrad in Rusland, werd gekenmerkt door de rivier de Pregel en zeven bruggen die twee eilanden met elkaar verbonden en de tegenoverliggende oevers met elkaar verbonden, waardoor de stad in vier zones werd verdeeld. Een intrigerende legende vertelt dat de inwoners een bijzondere uitdaging hadden: het vinden van een route die alle bruggen eenmaal overschreed. Een schijnbaar eenvoudige gedachte, maar niemand leek in staat te zijn deze opgave op te lossen.
Deze kwestie belandde uiteindelijk bij de wiskundige Leonhard Euler. Aanvankelijk was Euler niet overtuigd dat dit probleem een daadwerkelijk wiskundig karakter had, maar na het bestuderen van de kaart van de stad kreeg hij een belangrijke inval. Het maakte niet uit hoe men zich verplaatste tussen de vier zones van de stad (aangeduid als A, B, C en D), maar enkel de volgorde waarin de bruggen werden overschreden was van belang.
Hieruit volgde een briljante vereenvoudiging: de stukken land konden worden weergegeven als punten, en de bruggen als lijnen. Het probleem kon nu als volgt worden gevisualiseerd:
Verre van het besef van de gevolgen, was Euler bezig met het creëren van de basis van een nieuwe discipline: de grafentheorie. Deze is vandaag de dag van fundamenteel belang voor het bestuderen van patronen die kunnen worden gereduceerd tot elementen en verbindingen.
Een graaf is een eenvoudige manier om verbindingen weer te geven: hij bestaat uit punten (genaamd knopen) en lijnen die deze punten verbinden (genaamd takken). Door het systeem te analyseren, ontdekte Euler dat de mogelijkheid om alle bruggen precies één keer over te steken enkel afhing van het aantal lijnen dat elke knoop “raakte”, oftewel de graad van de knopen. Een dergelijke route – vandaag de dag een euleriaans pad genoemd – is mogelijk als:
- alle knopen een even graad hebben (dus een even aantal lijnen verbonden met het punt), of
- precies twee knopen een oneven graad hebben (start- en eindpunt).
Het probleem was echter dat in Königsberg alle vier de knopen een oneven graad hadden. Met andere woorden, de stedelijke uitdaging was vanaf het begin al onoplosbaar. Tot overmaat van rampspoed, zou de enige manier om de puzzel oplosbaar te maken zijn het verwijderen van ten minste één van de bruggen. Dit gebeurde daadwerkelijk, maar op tragische wijze: tijdens de Tweede Wereldoorlog werden delen van de stad en enkele bruggen verwoest door bombardementen, voordat Königsberg werd getransformeerd naar het huidige Kaliningrad.
De oplossing van Euler heeft echter veel langer overleefd dan de oorspronkelijke bruggen. Dit eenvoudige stedelijke raadsel leidde tot de ontwikkeling van de grafentheorie en, in bredere zin, tot een nieuwe manier van denken over vormen en verbindingen, en effende de weg voor de moderne topologie.